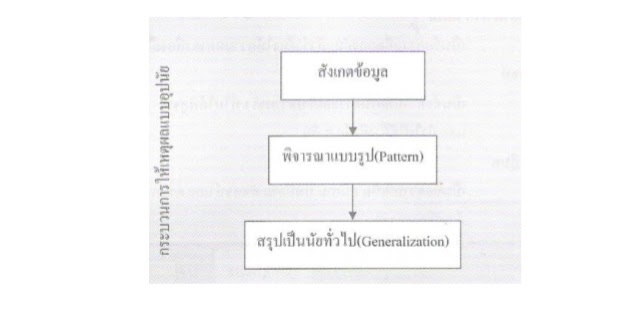
ตัวอย่างการให้เหตุผลแบบอุปนัย

1. มนุษย์สังเกตพบว่า : ทุก ๆวันดวงอาทิตย์ขึ้นทางทิศตะวันออก และตกทางทิศตะวันตก

จึงสรุปว่า : ดวงอาทิตย์ขึ้นทางทิศตะวันออก และตกทางทิศตะวันตกเสมอ

2. สุนทรี พบว่า ทุกครั้งที่คุณแม่ไปซื้อก๋วยเตี๋ยวผัดไทยจะมีต้นกุยช่ายมาด้วยทุกครั้ง

จึงสรุปว่า ก๋วยเตี๋ยวผัดไทยต้องมีต้นกุยช่าย

3. ชาวสวนมะม่วงสังเกตมาหลายปีพบว่า ถ้าปีใดมีหมอกมาก ปีนั้นจะได้ผลผลิตน้อย

เขาจึงสรุปว่าหมอกเป็นสาเหตุที่ทําให้ผลผลิตน้อย ต่อมามีชาวสวนหลายคนทดลองฉีดน้ำล้างช่อมะม่วง เมื่อมีหมอกมาก ๆ พบว่าจะได้ผลผลิตมากขึ้น จึงสรุปว่า การล้างช่อมะม่วงตอนมีหมอกมาก ๆ จะทําให้ได้ผลผลิตมากขึ้น

4. นายสมบัติ พบว่า ทุกครั้งที่ทำความดีจะมีความสบายใจ

จึงสรุปผลว่า การทำความดีจะทำให้เกิดความสบายใจ

ตัวอย่างการให้เหตุผลแบบอุปนัยทางคณิตศาสตร์

1. จงใช้การให้เหตุผลแบบอุปนัยสรุปผลเกี่ยวกับผลบวกของจํานวนคู่สองจํานวน

0 2 = 2 (จํานวนคู่)

2 4 = 6 (จํานวนคู่)

4 6 = 10 (จํานวนคู่)

6 8 = 14 (จํานวนคู่)

8 10 = 18 (จํานวนคู่)

สรุปผลว่า ผลบวกของจํานวนคู่สองจํานวนเป็นจํานวนคู่

2. 11 x 11 = 121

11 x 111 = 12321

1111 x 1111 = 1234321

11111 x 11111 = 123454321

3. (1 x 9) 2 = 11

(12 x 9) 3 = 111

(123 x 9) 4 = 1111

(1234 x 9) 5 = 11111

ข้อสังเกต

1) ข้อสรุปของการให้เหตุผลแบบอุปนัยอาจจะไม่จริงเสมอไป

2) การสรุปผลของการให้เหตุผลแบบอุปนัยอาจขึ้นอยู่กับประสบการณ์ของผู้สรุป

3) ข้อสรุปที่ได้จากการให้เหตุผลแบบอุปนัยไม่จําเป็นต้องเหมือนกัน

4) ข้อสรุปของการให้เหตุผลแบบอุปนัยอาจผิดพลาดได้

1.2. การให้เหตุผลแบบนิรนัย (Deductive reasoning)

เป็น การนําความรู้พื้นฐานที่อาจเป็นความเชื่อ ข้อตกลง กฏ หรือบทนิยาม ซึ่งเป็นสิ่งที่รู้มาก่อนและยอมรับว่าเป็นจริง เพื่อหาเหตุผลนําไปสู่ข้อสรุปการให้เหตุผลแบบนิรนัย ไม่ได้คํานึงถึง ความจริงหรือความเท็จ แต่จะคํานึงถึง เฉพาะข้อสรุปที่ต้องออกมาได้เท่านั้นพิจารณากระบวนการการให้เหตุผลแบบนิรนัย จากแผนภาพดังนี้

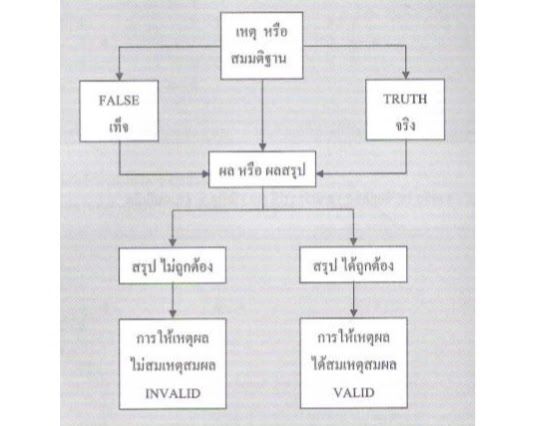
ตัวอย่างการให้เหตุผลแบบนิรนัย

1. เหตุ   1) จํานวนคู่หมายถึงจํานวนที่หารด้วย 2 ลงตัว
              2) 10 หารด้วย2 ลงตัว
                   ผล 10 เป็นจํานวนคู่
2. เหตุ 1) คนที่ไม่มีหนี้สินและมีเงินฝากในธนาคารมากกว่า 10 ล้านบาท เป็นเศรษฐี
           2) คุณมานะไม่มีหนี้สินและมีเงินฝากในธนาคาร 11 ล้านบาท
                 ผล คุณมานะเป็นเศรษฐี
3. เหตุ 1) นักกีฬาการแจ้งทุกคนจะต้องมีสุขภาพดี
            2) เกียรติศักดิ์เป็นนักฟุตบอลทีมชาติไทย
                ผล เกียรติศักดิ์มีสุขภาพดี
      จากตัวอย่างจะเห็นว่าการยอมรับความรู้พื้นฐานหรือความจริงบางอย่างก่อน แล้วจึงหาข่อสรุปจากสิ่งที่ยอมรับแล้วนั้น ซึ่งเรียกว่า ผล การสรุปผลจะถูกต้องก็ต่อเมื่อเป็นการสรุปผลได้อย่างสมเหตุสมผล  (valid) เช่น
      เหตุ  1) เรือทุกลําลอยน้ำ
              2) ถังน้ำพลาสติกลอยน้ําได้
                  ผล ถังน้ำพลาสติกเป็นเรือ
     การสรุปผลจากข้างต้นไม่สมเหตุสมผล แม้ว่าข้ออ้างหรือเหตุทั้งสองข้อจะเป็นจริง แต่การที่เราทราบ ว่า เรือทุกลําลอยน้ำได้ก็ไม่ได้หมายความว่าสิ่งอื่นๆ ที่ลอยน้ำได้จะต้องเป็นเรือเสมอไป ข้อสรุปในตัวอย่างข้างต้นจึงเป็นการสรุปที่ไม่สมเหตุสมผล

ข้อสังเกต  
     1. เหตุเป็นจริง และ ผลเป็นจริง
        เหตุ แมงมุมทุกตัวมี 6 ขาและสัตว์ที่มี 6 ขา ทุกตัวมีปีก
       ผล ดังนั้นแมงมุมทุกตัวมีปีก
2. เหตุเป็นเท็จ และ ผลเป็นเท็จ
    เหตุ ถ้านายดําถูกล็อตเตอรี่รางวัลที่หนึ่ง นายดําจะมีเงินมากมายแต่นายดําไม่ถูกล็อตเตอรี่รางวัลที่หนึ่ง
      ผล ดังนั้นนายดํามีเงินไม่มาก

3. เหตุอาจเป็นจริงและผลอาจเป็นเท็
4. ผลสรุปสมเหตุสมผลไม่ได้ประกันว่าข้อสรุปจะต้องเป็นจริงเสมอไป